板ポリを作ろう
板ポリはHoudini上でGridと呼ばれていて、
今回はsweepノードを使用して作成します。
sweepは
入力1:入力2の配置のベースになる形状
入力2:入力1の形状に配置したいオブジェクト
を繋げていきます。
詳しくはインディーゾーンさんのHoudini 18 SOP No.24 “Sweep:2.0 SOP”
が分かりやすくておすすめです。
まずsweepの入力1に繋がるノードを見ます。
lineでシンプルな線を作成します。
ポイント数は後のノードで増やしていくので今は2個にしておきます。
入力2に繋がるノードを見ていきます。
数値が多少変わるだけでやることは一緒です。
lineでシンプルな線を作成して
resampleでlineのポイントを増やすだけです。
(Lengthの値は入力1より小さくしています。)
最後に入力1と入力2をそれぞれsweepにつなぎます。
これで板ポリができます。
イメージはお互いラインが格子状に配置されている感じです。
※今回はイメージしやすいように「格子状に配置されている」と書いてますが、正確には「2番目の入力から断面曲線を受け取り、1番目の入力の背骨曲線に沿ってその断面曲線のコピーを分布させて、その分布させた断面曲線間にサーフェスを作成する」処理が行われているので注意!
UVs and AttributesのCompute UVsにだけチェックを入れておきます。
UVを自動で作成してくれます。
これでGridの作成は完了です。
VEXを書いてみよう
次はVEXを記述していきます。
Attributewrangleを、左のresampleの下に繋ぎます。
VEXpressionという欄に以下を記述していきます。
@Alpha = chramp(“Alpha”, fit(@ptnum, 0,@numpt-1, 0, 1));
いったんコピペで大丈夫です。
細かく中身を見ていきましょう。
@Alphaはポイントのアルファ情報を意味しています。
fitは「ある範囲内の値を別の範囲内に置き換える、フィットさせる」関数です。
例えばfit(10, 5,15, 0,1)だった場合、
元の値が範囲 [5, 15] から範囲 [0, 1] に変換されます。
つまり、元の値 10 は範囲 [5, 15] で中間の位置にあるため、
fit() 関数によって範囲 [0, 1] での中間の値に置き換えられます。
よってfit(10, 5,15, 0,1);の結果は0.5になります。

あらためて今回の場合を見ていきます。
置き換えたい値:@ptnum
@ptnumはそれぞれのポイントに順番に振られている番号で0~10まで振られてます。
元の範囲:0,@numpt-1
@numptというのはポイントの総数で、今回だと11になります。
そこから1をひくので 11-1=10。@numpt-1=10ということになります。
置き換え後の範囲:0, 1
これはそのまま0から1になります。
これで@ptnumは0~1の範囲に置き換えられました。
それを「@Alpha=」でAlpha値に代入します。
最終的な結果はGeometry Spreadsheetを確認してみましょう。
各ポイントAlphaに0~1の値が割り振られていることが分かります。
ちなみに1つ上のresampleノードでポイントの数を増やしたとしても、
その全てのポイントにちゃんと0~1の値が割り振られていることが確認できます。
ここまで説明しておいて何ですが
なぜポイントを0~1の範囲に収める必要があるか?
…を書いていませんでした。
それはchramp(カーブ)が0~1の範囲しか扱えないからです。
そのため、今回のように複数のポイントを扱う場合はfit関数で範囲を置き換える必要があります。
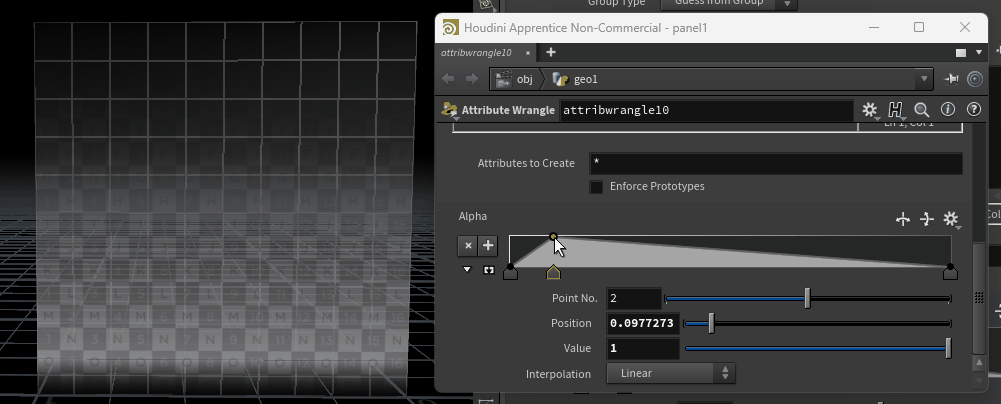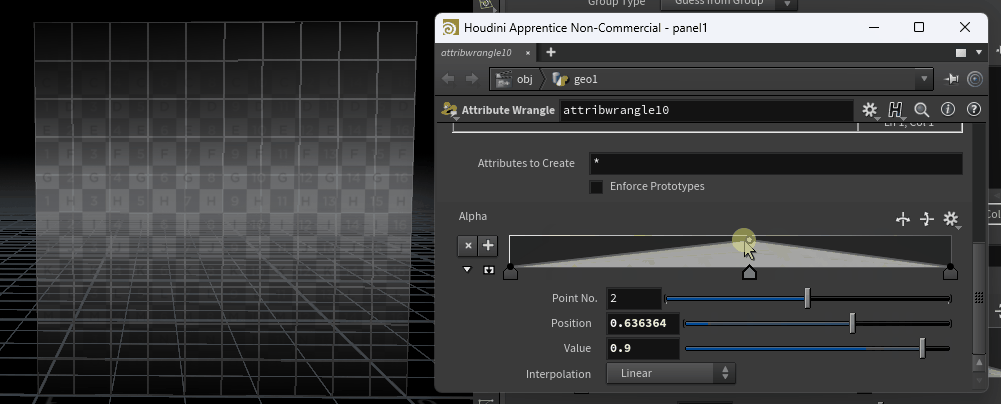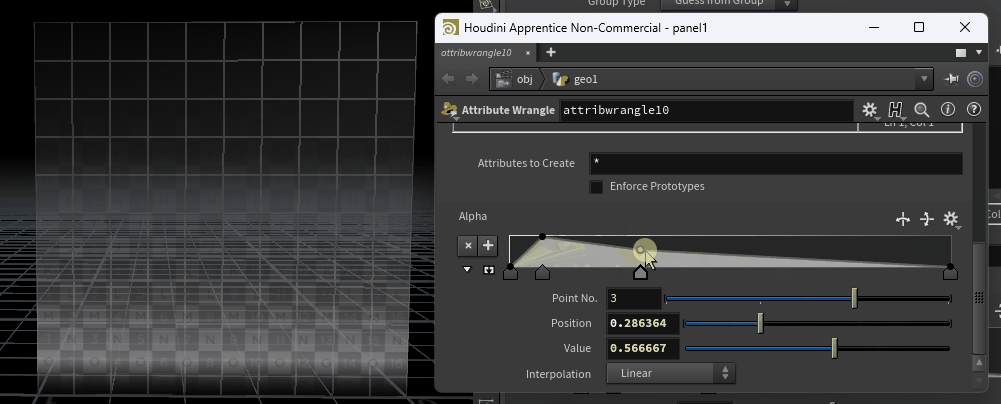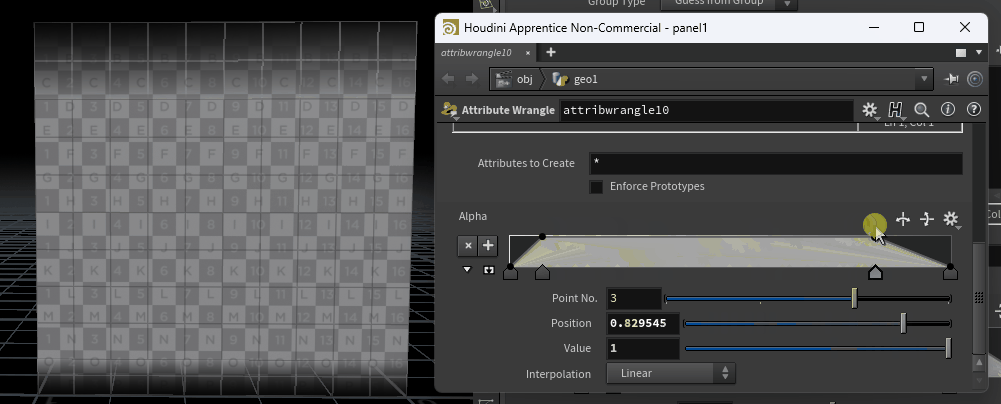
次に、chrampについてです。
前述したfit関数を覆うようにchramp関数を記述します。
“Alpha“はカーブの名前を決めるだけのものなので、“hogehoge”でも何でもOKです。
今回は分かりやすくするためにAlphaと付けておきます。
…出来てはいますが見づらいですね。Visualizeノードを使用して色をつけて確認してみます。
attributewrangleにvisualizeを繋いで、
するとColorRampに基づいて「0に近いほど紫に / 1に近いほど赤に 」表示になります。
これで結果が分かりやすくなったと思います。

これで全ての作業は完了しました!