❏ はじめに
この記事では、MayaのBifrostを使用した『プロシージャルなUV制御』をご紹介します。
Bifrostを使用することで、下記動画のようにUV制御(回転、バイアス、シアー)ができます。
※処理単体の解説はしますが、処理を繋げる方法やコンパウンド化については触れません。
❐ 自作コンパウンド
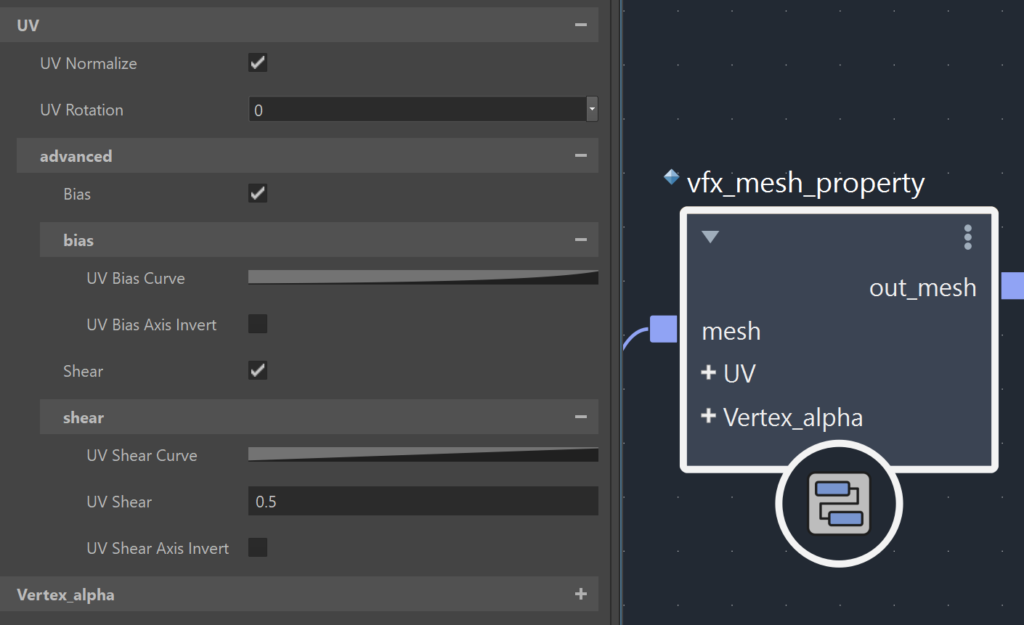
冒頭の動画は私が作成したコンパウンド「vfx_mesh_property」の動画です。
エフェクトメッシュでは「UV・頂点カラー」の制御が頻出します。それらの作業を Bifrost でプロシージャルに行うためのコンパウンドです。
コンパウンド化することでチーム内で「共有・管理・運用」がしやすくなります。
❐ Bifrost でUV処理をするメリット
・頂点数が変わっても制御が崩れない

MayaでUVを制御する際、通常は配列をもとに処理がされます。
簡単に言うと「各頂点のUV位置」を「 0, 1, 2, ~~」の番号と紐づけて処理をしています。
そのため、頂点数を変更するとこの位置と番号の関係が崩れ左画像のようにぐちゃぐちゃになります。
Bifrost は処理ごとに配列を更新しているため、頂点数を変えても処理が壊れません。
❐ 基本の処理
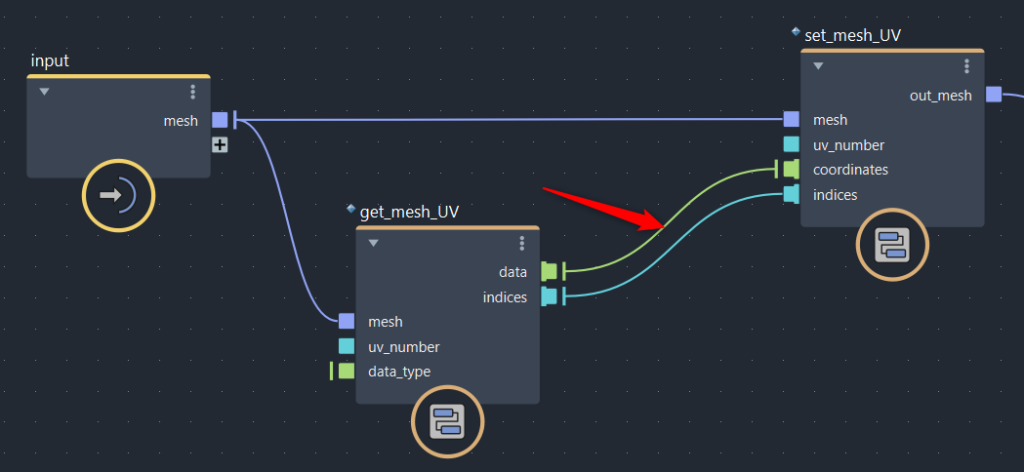
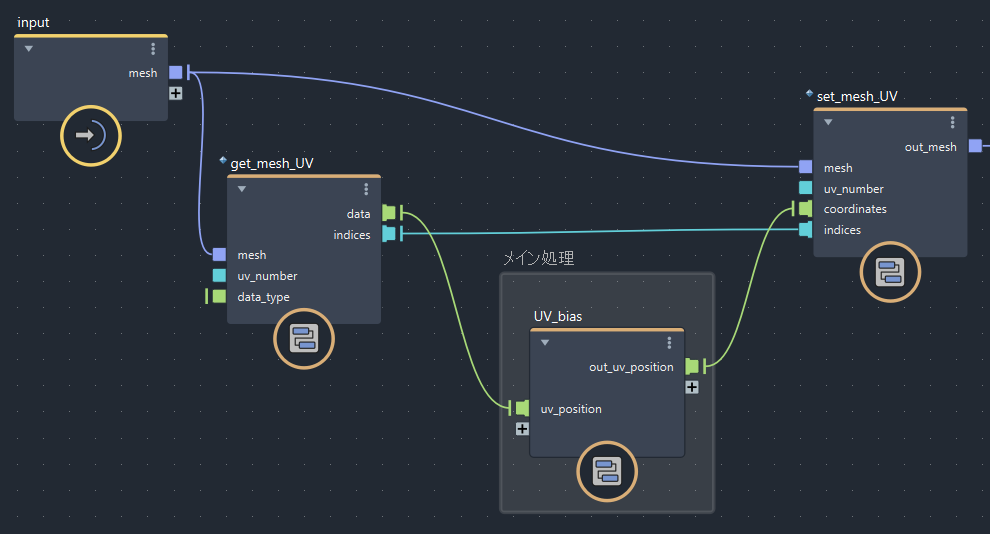
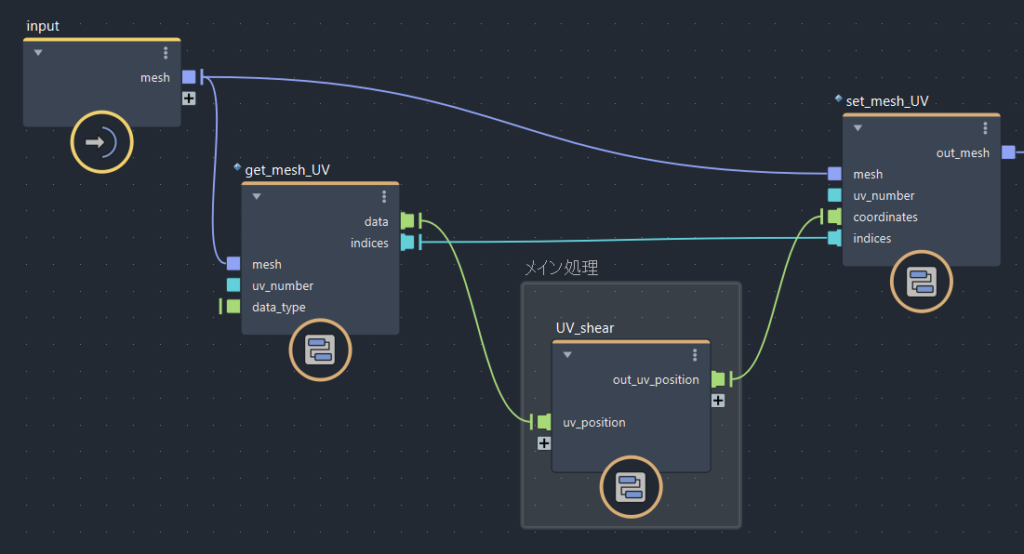
・「get_mesh_UV」:メッシュのUV情報を取得
・「set_mesh_UV」:UV情報をメッシュに格納
緑色の線がUV座標(Vector2の配列)です。この部分に処理を加えてUVを加工していきます。
水色の線( indices )は画像のとおりに繋いでください。詳しい説明は省きますが、ここを繋いでいないと処理が崩れる場合があります。
① UVの回転
いくつか方法がありますが、[Substance Designer]の 「Non Uniform Rotation」で使用されていた処理を紹介します。
( 2次元回転行列はノードベースだと線がぐちゃぐちゃして見えるので… )
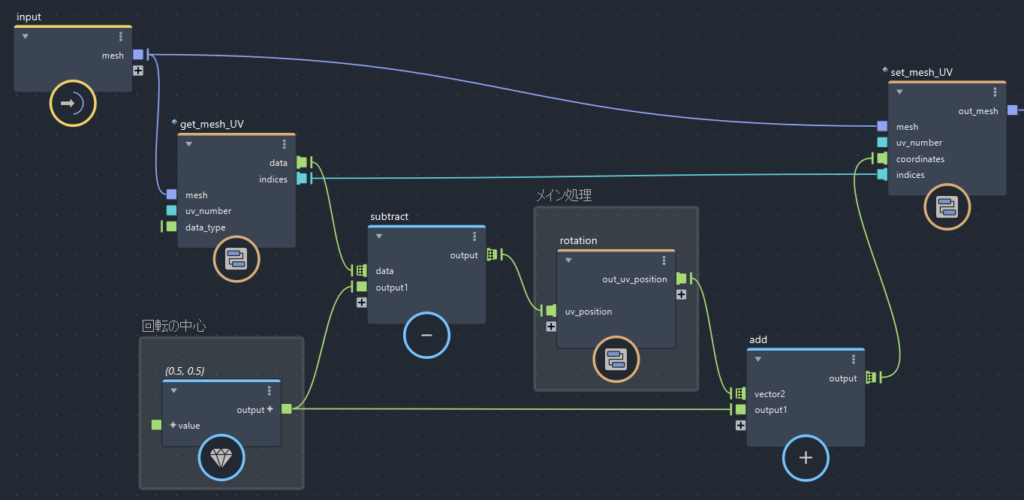
【処理の全体像】
- あらかじめUV座標から(0.5, 0.5)を減算
- 回転処理
- 回転したUV座標に(0.5, 0.5)を加算し、もとの位置に戻す
メイン処理(rotation)は原点(0, 0)を中心に処理が行われます。
そのため、正規化されたUVの中心(0.5, 0.5)で回転させたい場合は[1、3]の手順が必要。
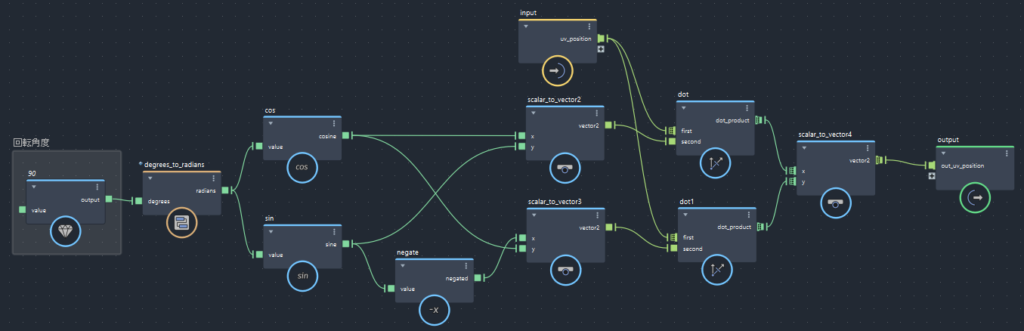
【メイン処理(rotationノード)の中身】
- 回転角度を入力
- 「degrees_to_radians」で度数からラジアンへ変換
- cosineとsineを求め、それをもとに2つのベクトルを作成
- UV座標で内積を取り、回転されたUV座標(Vector2)を作成
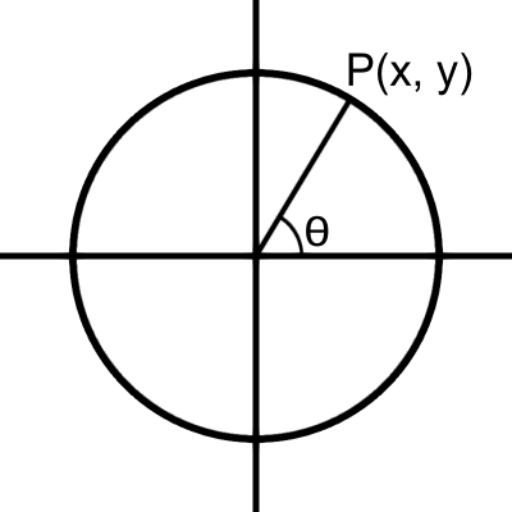
(ちなみに⇧の図はSubstanceDesignerで作りました。SD最高!)
左の図において、r = 1とするとP(x, y) = (cosθ, sinθ)
よって、 cosθとsinθをもとに作られたベクトルの長さは”1”です。
また、右の動画の矢印が cosθとsinθをもとに作られた二本のベクトルです。
回転角度を増加させると反時計回りに回転します。
赤矢印 =(cosθ, sinθ)
緑矢印(入力ベクトル) =(1, 0)
青矢印 = dot(内積)の値
dot(内積)は単純に言うと『2つのベクトルがどれだけ同じ方向を向いているか』を表しています。
“赤矢印の長さ = 1 ” のため、dot から返される値は(-入力ベクトルの長さ ~ 入力ベクトルの長さ)に収まります。
つまり、赤矢印と緑矢印が同じ向きのとき、”青矢印の長さ = 緑矢印の長さ” となります。
| 緑矢印(入力ベクトル) | (1, 0) | (0.5, 0.5) | (0, 1) | |||
|---|---|---|---|---|---|---|
| 回転角度, 赤矢印 | 角度 | 内積 | 角度 | 内積 | 角度 | 内積 |
| ii0°,(1, 0) | 0° | 1 | 45° | 0.5 | 90° | 0 |
| iiiiii90°,(0.5, 0.5) | 90° | 0 | 45° | 0.5 | 0° | 1 |
| 180°, (0, 1) | 180° | -1 | 135° | -0.5 | 90° | 0 |
| iiiiiiii270°,(-0.5, -0.5) | 90° | 0 | 135° | -0.5 | 180° | -1 |
「赤矢印と緑矢印の内積と角度」は上の表のようになります。
例えば、回転角度が「0°」のときは赤矢印 =(1, 0)となり、緑矢印(1, 0)との角度はベクトルの向きが等しいため0°です。
内積 = 『2つのベクトルがどれだけ同じ方向を向いているか』= ” 1 ” となります。
※当然入力ベクトルによって内積の結果は異なります。
また、回転角度が0°の入力ベクトルと内積を見ると「入力ベクトルのX座標 = 内積」であることがわかります。
他の角度もみていくと「回転角度の分だけ回転させた位置のX座標 = 内積」となっています。
Y座標は「赤矢印 =(-sinθ, cosθ) = (cosθ, sinθ)を反時計回りに90°回転した値」で計算することで求めることができます。
② UVのバイアス
【処理の全体像】
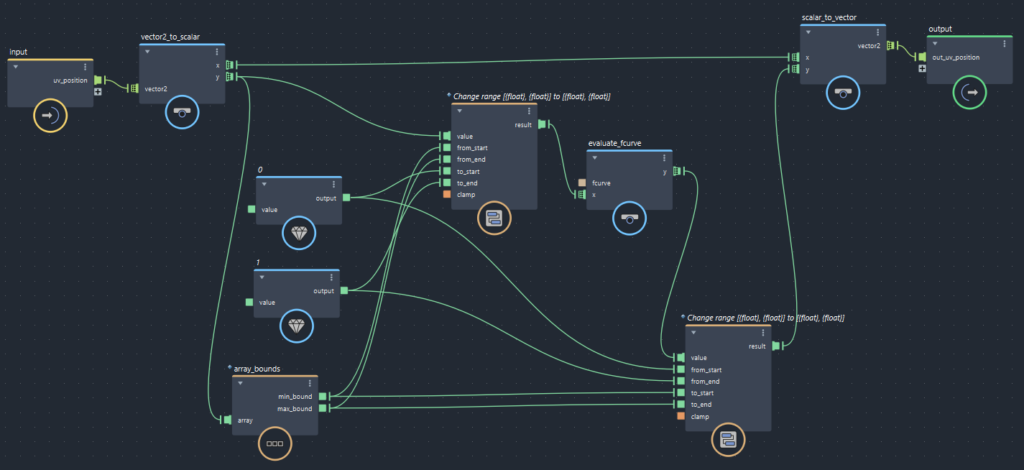
【メイン処理(UV_biasノード)の中身】
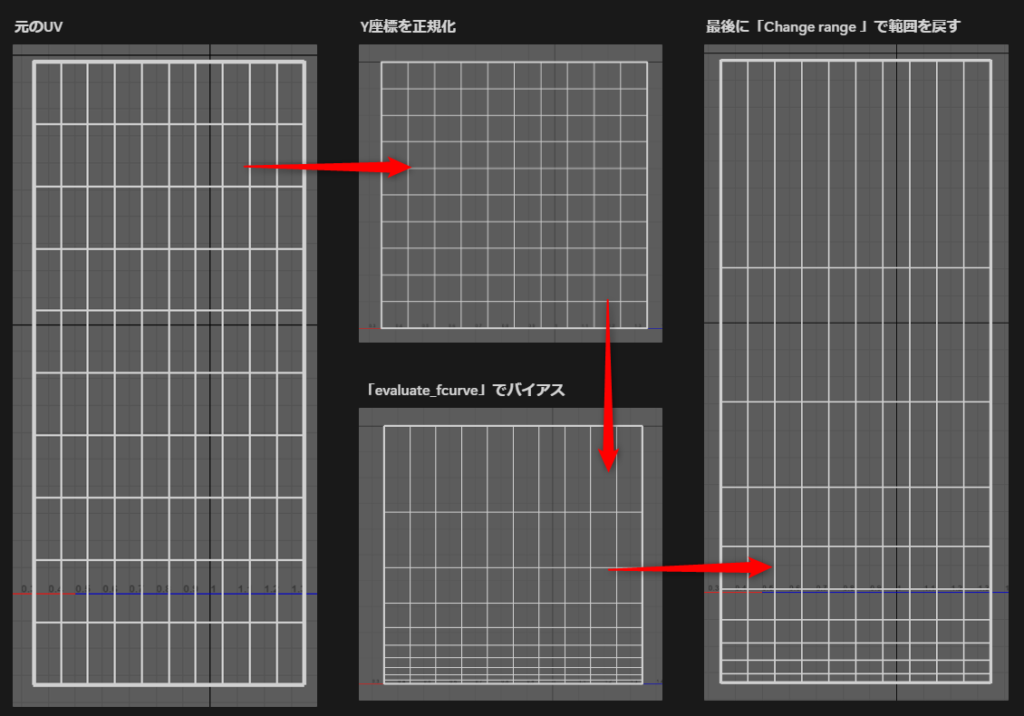
【UVの形状の流れ】
- UVのY座標を正規化
- 「evaluate_fcurve」で値をリマップ
- 元のUVの最大値と最小値をもとの大きさに戻す
「Change range 」は入力 value の範囲を to_start から to_end までの期間で同じ比率となる値を返します。
「array_bounds 」は入力配列の最小値と最大値を取得できます。
難しく考えずに「Change range 」と「array_bounds 」を用いて、『配列の値を任意の値の範囲に収めることができる』とご理解いただければ問題ありません。
身近なところでいうと、UVの正規化と同じ処理です。今回の場合は、UVのY座標を” 0~1 “に正規化しています。
値が正規化されていることで「evaluate_fcurve」で処理ができます。
このノードは上の動画のようにカーブで値をグラフィカルに操作でき、UVのバイアスをかけるメインの処理になります。
最後に「Change range 」で元のUVのY座標の範囲に戻します。
現在はY座標が正規化されているため元のUVと異なる範囲になっています。
そのために、最初に行った「最小値と最大値を元に” 0~1 “の範囲に収める」の逆をします。つまり、「” 0~1 “の値を初期の最小値と最大値の範囲に戻す」です。
これにより、UVのバイアスだけ行ったUV座標を取得できます。
③ UVのシアー
【処理の全体像】
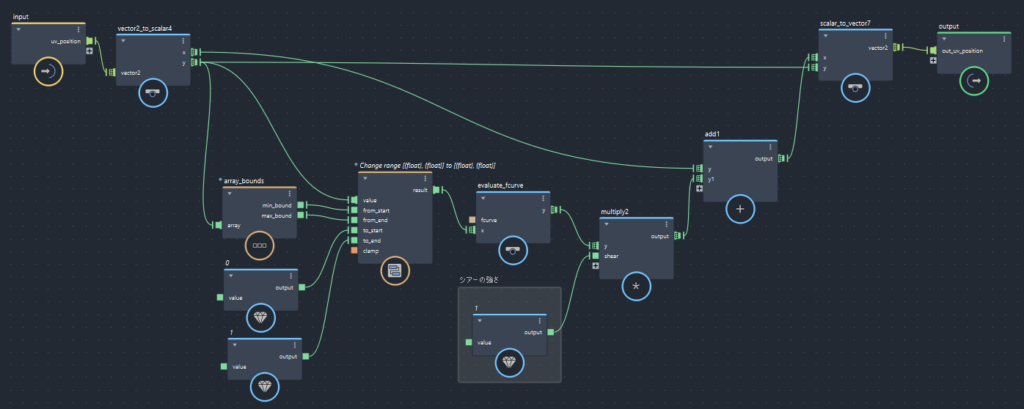
【メイン処理(UV_shearノード)の中身】
- UVのY座標を正規化
- 「evaluate_fcurve」で値をリマップ、係数をかける
- 元のUVのX座標に加算
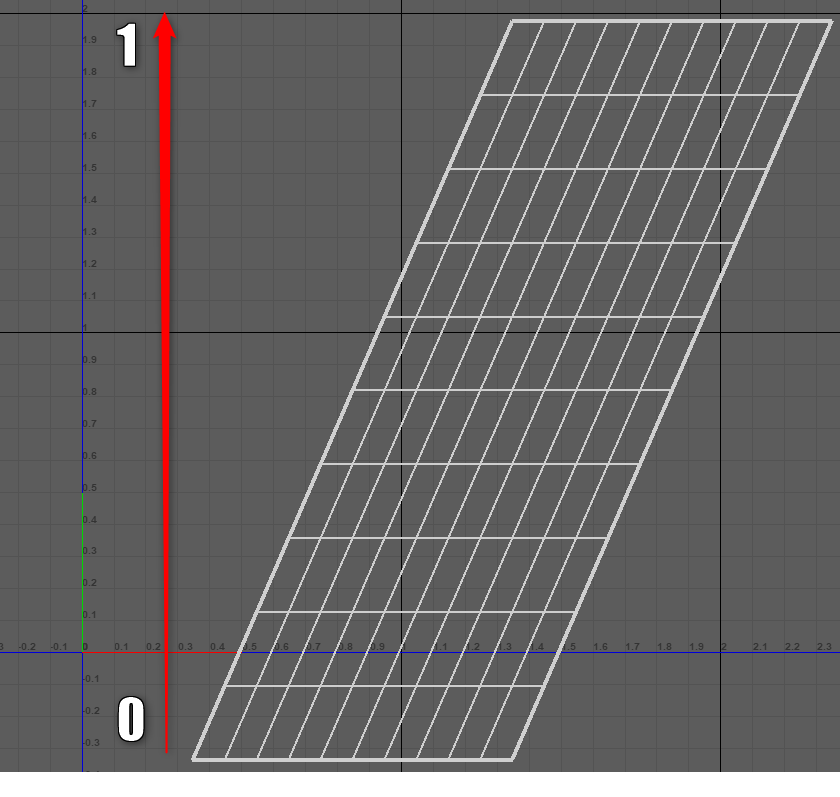
まず、UVのバイアスと同じように値を正規化します。この時点でシアーは作成できます。
Y座標が高いほど値が ” 0 → 1 ” に遷移し、それを「元のUVのX座標に加算」すると画像のようになります。
これだけだと作れる形状があまりに限定的なので処理を追加します。
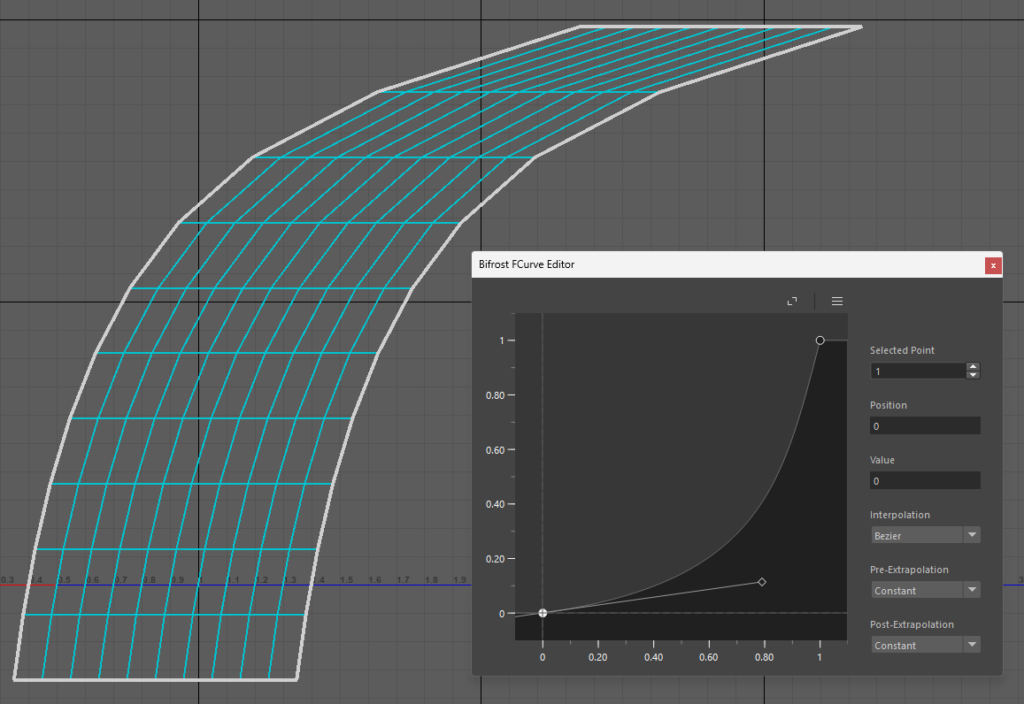
「evaluate_fcurve」で値をリマップします。これにより曲線的なシアーをかけることができます。
(曲線的なシアーを使う機会は稀だと思いますが、紹介だけさせていただきます。)
そこに係数をかけ、シアーの強度を設定します。
上の画像では「evaluate_fcurve」で値を調整し、係数に” 2 “をかけています。
係数が ” 0 “でシアーが完全にかからなくなり、係数が大きくなるほどより強くシアーがかかります。
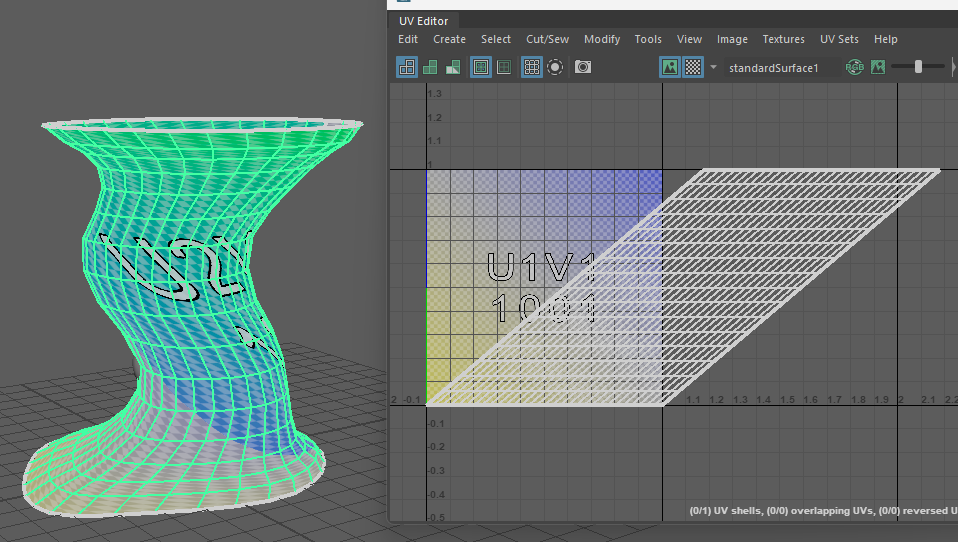
例えば、CylinderメッシュのUVにシアーをかけることで、メッシュをTwistさせるよりもきれいにテクスチャを貼れます。(テクスチャの歪みが少ない)
UVの形状を工夫することで、処理負荷をかけずに複雑さを出すことができます。
❏まとめ
・Bifrost ではUVを「プロシージャル」かつ「グラフィカル」に処理できる
・sine, cosine などはなんとなく程度の理解でも役に立つ
Bifrostには便利な計算ノードが標準で用意されており、アーティストでも簡単に処理が組めます。
難しい部分は先人たちが使いやすい形で現代に残してくれていますので、『なんとなくの抵抗感』でやらないのはもったいないです!
日頃の作業で効率化できるところは必ずあるので、積極的に改善していきましょう!